2. PRFs, PRPs and Block Ciphers

Pseudorandom Functions (PRF)

Definition. A pseudorandom function $F$ over $(\mathcal{K}, X, Y)$ is an efficiently computable algorithm $F : \mathcal{K} \times X \rightarrow Y$.

We consider a keyed function $F : \mathcal{K} \times X \rightarrow Y$ where $\mathcal{K}$ denotes the key space. For $k \in \mathcal{K}$, $F_k(x) := F(k, x)$ is a function from $X$ to $Y$. Thus each key $k$ induces a distribution on functions $X \rightarrow Y$.

Note that $\left\lvert \mathcal{F}[X, Y] \right\lvert = \left\lvert Y \right\lvert^{\left\lvert X \right\lvert}$, but the number of PRFs is at most $\left\lvert K \right\lvert$. In practice, $\left\lvert K \right\lvert$ is very small compared to $\left\lvert Y \right\lvert^{\left\lvert X \right\lvert}$. So PRFs are chosen from a smaller space, but they should behave in the same way a (truly) random function does.

Let $\mathcal{F}[X, Y]$ denote the set of all functions from $X$ to $Y$. A PRF $F$ would be secure if it is indistinguishable from a random function in $\mathcal{F}[X, Y]$. This notion is formalized as a security game.

Definition. Let $F$ be a PRF defined over $(\mathcal{K}, X, Y)$. For an adversary $\mathcal{A}$, define two experiments 0 and 1.

Experiment $b$.

1. The challenger selects $f \in \mathcal{F}[X, Y]$ as follows
   • If $b = 0$, choose $k \leftarrow \mathcal{K}$ and set $f = F_k = F(k, \cdot)$.
   • If $b = 1$, choose $f \leftarrow \mathcal{F}[X, Y]$.
2. The adversary sends a sequence of queries to the challenger.
   • For $i = 1, \dots, q$, send $x_i \in X$ and receive $y_i = f(x_i) \in Y$.
3. The adversary computes and outputs a bit $b’ \in \left\lbrace 0, 1 \right\rbrace$.

Let $W_b$ be the event that $\mathcal{A}$ outputs 1 in experiment $b$. Then the PRF-advantage of $\mathcal{A}$ with respect to $F$ is defined as

\[\mathrm{Adv}_{\mathrm{PRF}}^q[\mathcal{A}, F] = \left\lvert \Pr[W_0] - \Pr[W_1] \right\lvert.\]

A PRF $F$ is secure if $\mathrm{Adv}_{\mathrm{PRF}}^q[\mathcal{A}, F]$ is negligible for any efficient $\mathcal{A}$.

In experiment $0$ above, the challenger returns $y_i = f(x_i)$. To answer the query $x_i$, the challenger would have to keep a lookup table for a random function $f \in \mathcal{F}[X, Y]$. Since $X$ and $Y$ are very large in practice, it is nearly impossible to create and manage such lookup tables.¹ As a workaround, we can choose $y_i$ uniformly on each query $x_i$, assuming that $x_i$ wasn’t queried before. This is possible since for any different inputs $x_i, x_j \in X$, $f(x_i)$ and $f(x_j)$ are random and independent.

Also, there are two ways that the adversary can query the challenger. The first method is the adaptive method, where the adversary queries each $x_i$ one by one. In this method, the adversary can adaptively choose the next query $x_{i+1}$ after receiving the result from the challenger.

The second method is querying all $x_i$ at once. We will consider the first method, since the adaptive method assumes greater attack power on the adversary.

OTP as a PRF

As an example, consider the one-time pad function $F(k, x) = k \oplus x$. This function satisfies the definitions of PRFs, but it is not a secure PRF. Consider an adversary $\mathcal{A}$ that outputs $1$ if and only if $y_1 \oplus y_2 = x_1 \oplus x_2$. In experiment $0$, $\mathcal{A}$ will always output $1$, but in experiment $1$, $\mathcal{A}$ will output $1$ with probability $2^{-n}$. Thus the advantage is $1 - 2^{-n}$, which is not negligible.

PRFs and PRGs

It is easy to construct PRGs from PRFs. We can simply evaluate $F$ on some distinct inputs. For example, given a seed $s$, we evaluate $F_s$ and obtain

\[G(s) = F_s(1) \parallel F_s(2) \parallel \cdots \parallel F_s(n)\]

for any $n \in \mathbb{N}$.² In fact, we can show that $G$ is secure PRG if $F$ is a secure PRF.

Theorem. If $F$ is a secure length preserving PRF, then $G$ in the above definition is a secure PRG.

Proof. Suppose that $\mathcal{A}$ is an efficient PRG adversary against $G$. We construct an efficient $n$-query PRF adversary $\mathcal{B}$, that queries the challenger at $1, \dots, n$ and receives $f(1), \dots, f(n)$. $\mathcal{B}$ passes $f(1) \parallel \cdots \parallel f(n)$ to $\mathcal{A}$, and $\mathcal{B}$ outputs the output of $\mathcal{A}$. Then we see that $\mathrm{Adv}{\mathrm{PRG}}[\mathcal{A}, G] = \mathrm{Adv}{\mathrm{PRF}}[\mathcal{B}, F]$. So if $F$ is secure, then $G$ is secure.

As for the converse, a PRG $G$ gives a PRF $F$ with small input length. If $G : \left\lbrace 0, 1 \right\rbrace^n \rightarrow \left\lbrace 0, 1 \right\rbrace^{n 2^m}$, we can define a PRF $F : \left\lbrace 0, 1 \right\rbrace^n \times \left\lbrace 0, 1 \right\rbrace^m \rightarrow \left\lbrace 0, 1 \right\rbrace^n$ as follows: for a seed $s \in \left\lbrace 0, 1 \right\rbrace^n$, consider $G(s)$ as a $2^m \times n$ table and set $F(s, i)$ as the $i$-th row of $G(s)$.³ If $G$ is a secure PRG, then PRF $F$ is also secure.

Pseudorandom Permutations (PRP)

Definition. A pseudorandom permutation $E$ over $(\mathcal{K}, X)$ is an efficiently computable algorithm $E : \mathcal{K} \times X \rightarrow X$ that has an efficient inversion algorithm $D$ such that $D(k, E(k, x)) =x$.

Permutations defined on a set $X$ are bijections on $X$, so a PRP $E(k, \cdot)$ is one-to-one for all $k \in \mathcal{K}$, and also has an inverse function.

Similarly, a PRP $E$ is secure if it is indistinguishable from a random permutation on $X$. Let $\mathcal{P}[X]$ denote the set of all permutations on $X$.

Definition. Let $E$ be a PRP defined over $(\mathcal{K}, X)$. For an adversary $\mathcal{A}$, define two experiments $0$ and $1$.

Experiment $b$.

1. The challenger selects $f \in \mathcal{P}[X]$ as follows
   • If $b = 0$, choose $k \leftarrow \mathcal{K}$ and set $f = E_k = E(k, \cdot)$.
   • If $b = 1$, choose $f \leftarrow \mathcal{P}[X]$.
2. The adversary sends a sequence of queries to the challenger.
   • For $i = 1, \dots, q$, send $x_i \in X$ and receive $y_i = f(x_i) \in Y$.
3. The adversary computes and outputs a bit $b’ \in \left\lbrace 0, 1 \right\rbrace$.

Let $W_b$ be the event that $\mathcal{A}$ outputs 1 in experiment $b$. Then the PRP-advantage of $\mathcal{A}$ with respect to $E$ is defined as

\[\mathrm{Adv}_{\mathrm{PRP}}^q[\mathcal{A}, E] = \left\lvert \Pr[W_0] - \Pr[W_1] \right\lvert.\]

A PRP $E$ is secure if $\mathrm{Adv}_{\mathrm{PRP}}^q[\mathcal{A}, E]$ is negligible for any efficient $\mathcal{A}$.

PRF Switching Lemma

Suppose that $\left\lvert X \right\lvert$ is sufficiently large. Then for $q$ queries of any adversary $\mathcal{A}$, it is highly probable that $f(x_i)$ are all distinct, regardless of whether $f$ is a PRF or a PRP. Thus we have the following property of PRPs.

Lemma. If $E: \mathcal{K} \times X \rightarrow X$ is a secure PRP and $\left\lvert X \right\lvert$ is sufficiently large, then $E$ is also a secure PRF.

For any $q$-query adversary $\mathcal{A}$,

\[\left\lvert \mathrm{Adv}_{\mathrm{PRF}}[\mathcal{A}, E] - \mathrm{Adv}_{\mathrm{PRP}}[\mathcal{A}, E] \right\lvert \leq \frac{q^2}{2\left\lvert X \right\lvert}.\]

This is a matter of collisions of $f(x_i)$, so we use the facts from the birthday problem.

Proof. Appendix A.4.

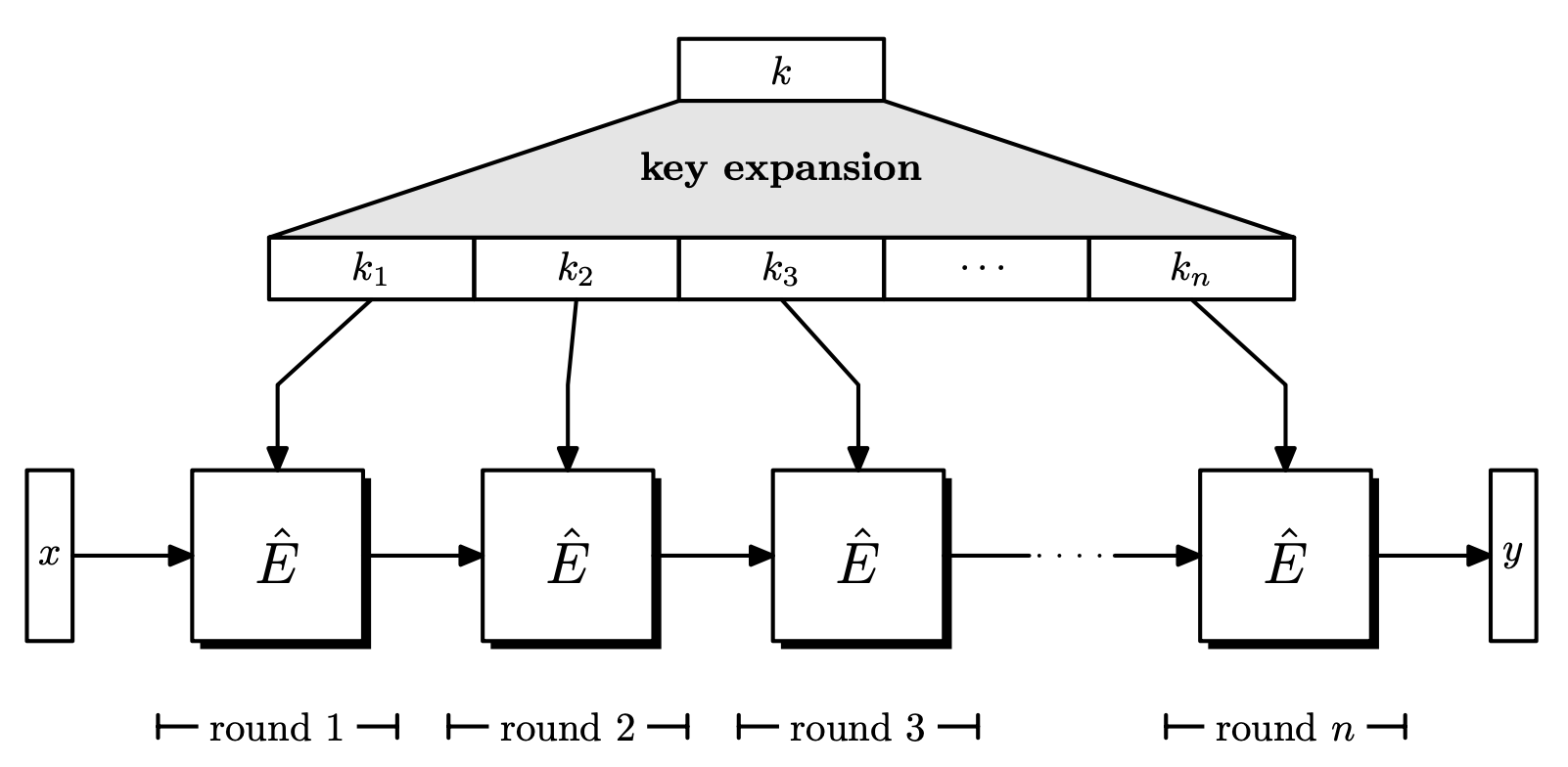
Block Ciphers

A block cipher is actually a different name for PRPs. Since a PRP $E$ is a keyed function, applying $E(k, x)$ is in fact encryption, and applying its inverse is decryption.

Block ciphers commonly have the following form.

• A key $k$ is chosen uniformly from $\left\lbrace 0, 1 \right\rbrace^s$.
• The key $k$ goes through key expansion and generates $k_1, \dots, k_n$. These are called round keys, where $n$ is the number of rounds.
• The plaintext goes through $n$ rounds, where in each round, a round function and the round key is applied to the input.
• After $n$ rounds, the ciphertext is obtained.

Data Encryption Standard (DES)

Brief History

• 1972: NIST calls for a block cipher standard (proposal).
• 1974: Horst Feistel (IBM) designs Lucifer, which evolves into DES.
• 1976: DES is standardized and widely implemented.
• 1997: DES is broken by exhaustive search.
• 2001: DES is replaced by AES.

Feistel Network

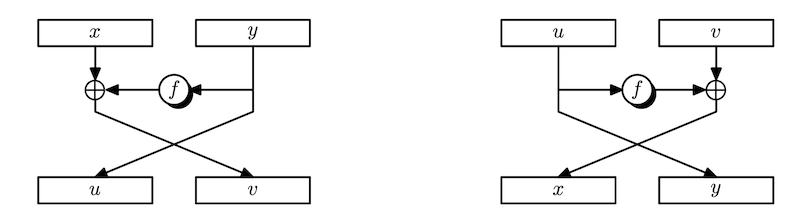
Since block ciphers are PRPs, we have to build an invertible function. Suppose we are given any functions $F_1, \dots, F_d : \left\lbrace 0, 1 \right\rbrace^n \rightarrow \left\lbrace 0, 1 \right\rbrace^n$. Can we build an invertible function $F : \left\lbrace 0, 1 \right\rbrace^{2n} \rightarrow \left\lbrace 0, 1 \right\rbrace^{2n}$?

It turns out the answer is yes. Given an $2n$-bit long input, $L_0$ and $R_0$ denote the left and right halves ($n$ bits) of the input, respectively. Define

\[L_i = R_{i-1}, \qquad R_i = F_i(R_{i-1}) \oplus L_{i-1}\]

for $i = 1, \dots, d$. Then we can restore $L_0$ and $R_0$ from $L_d$ and $R_d$ by applying the same operations in reverse order. It is easy to see that $R_{i-1}$ can be restored from $L_i$. As for $L_{i-1}$, we need a swap. Observe that

\[F_i(L_i) \oplus R_i = F_i(R_{i-1}) \oplus (F_i(R_{i-1}) \oplus L_{i-1}) = L_{i-1}.\]

Note that we did not require $F_i$ to be invertible. We can build invertible functions from arbitrary functions! These are called Feistel networks.

Theorem. (Luby-Rackoff’85) If $F : K \times \left\lbrace 0, 1 \right\rbrace^n \rightarrow \left\lbrace 0, 1 \right\rbrace^n$ is a secure PRF, then the $3$-round Feistel using the functions $F_i= F(k_i, \cdot)$ is a secure PRP.

In DES, the function $F_i$ is the DES round function.

The Feistel function takes $32$ bit data and divides it into eight $4$ bit chunks. Each chunk is expanded to $6$ bits using $E$. Now, we have 48 bits of data, so apply XOR with the key for this round. Next, each $6$-bit block is compressed back to $4$ bits using a S-box. Finally, there is a permutation $P$ at the end, resulting in $32$ bit data.

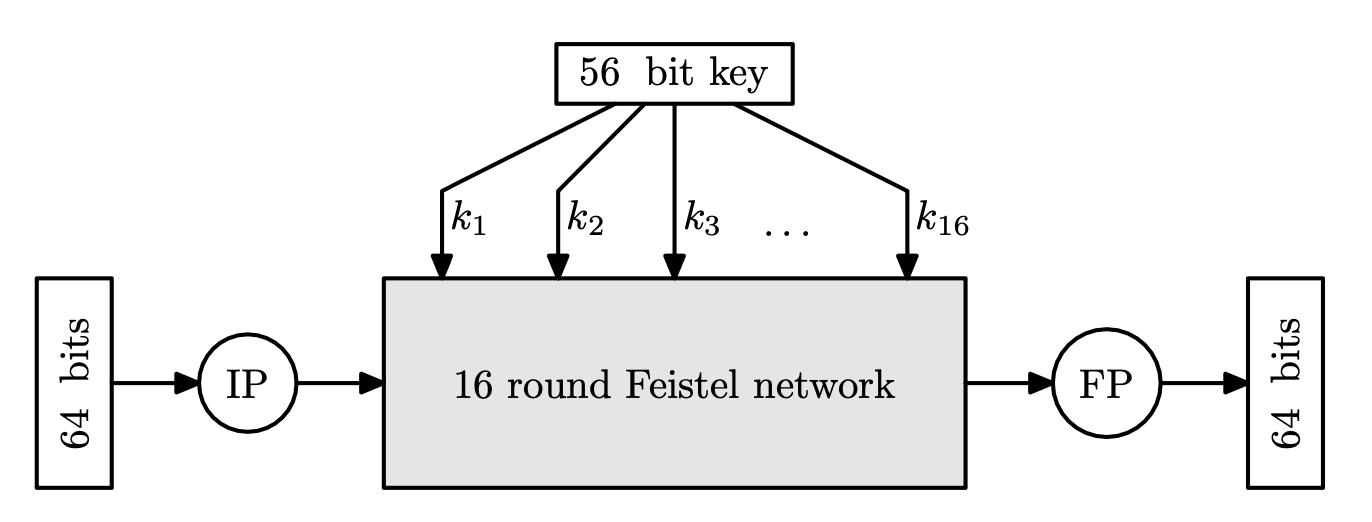
DES Algorithm

DES uses $56$ bit keys that generate $16$ rounds keys. The diagram below shows that DES has 16-round Feistel networks.

The input goes through initial/final permutation, which are inverses of each other. These have no cryptographic significance, and just for engineering.

Advanced Encryption Standard (AES)

DES is not secure, since key space and block length is too small. Thankfully, we have a replacement called the advanced encryption standard (AES).

• DES key only had $56$ bits, so DES was broken in the 1990s
• NIST standardized AES in 2001, based on Rijndael cipher
• AES has $3$ different key lengths: $128$, $192$, $256$
  • Different number of rounds for different key lengths
  • $10$, $12$, $14$ rounds respectively
• Input data block is $128$ bits, so viewed as $4\times 4$ table of bytes
  • This table is called the current state.

Each round consists of the following:

• SubBytes: byte substitution, 1 S-box on every byte
• ShiftRows: permutes bytes between groups and columns
• MixColumns: mix columns by using matrix multiplication in $\mathrm{GF}(2^8)$.
• AddRoundKey: XOR with round key

Modules

SubBytes

• A simple substitution of each byte using $16 \times 16$ lookup table.
• Each byte is split into two $4$ bit nibbles
  • Left half is used as row index
  • Right half is used as column index

ShiftRows

• A circular bytes shift for each row, so it is a permutation
• $i$-th row is shifted $i$ times to the left. ($i = 0, 1, 2, 3$)

MixColumns

• For each column, each byte is replaced by a value
  • The value depends on all 4 bytes of the column
• Each column is processed separately
  • Thus effectively, it is a matrix multiplication (Hill cipher)

AddRoundKey

• XOR the input with $128$ bits of the round key
  • The round key is different for each round

These 4 modules are all invertible!

Attacks on Block Ciphers

DES S-box

For DES, the S-box is the non-linear part. If the S-box is linear, then the entire DES cipher would be linear.

Specifically, there would be a fixed binary matrix $B _ 1 \in \mathbb{Z} _ 2^{64 \times 64}$ and $B _ 2 \in \mathbb{Z} _ 2^{64 \times (48 \times 16)}$ such that

\[\mathrm{DES}(k, m) = B_1 m \oplus B_2 \mathbf{k}\]

where $\mathbf{k} \in \mathbb{Z}_2^{48 \times 16}$ is a vector of round keys.

Then we can attack DES with the same idea as OTP. If $c_i = B_1 m_i \oplus B_2 \mathbf{k}$, then $c_1 \oplus c_2 = B_1 (m_1 \oplus m_2)$.

Choosing the S-boxes at random results in a insecure block cipher, with high probability.

Strengthening Ciphers Against Exhaustive Search

For DES (and AES-128), it is known that three pairs of plaintext, ciphertext blocks are enough to ensure that there is a unique key mapping the given plaintext to the ciphertext, with high probability. We assume here that we are given plaintext, ciphertext block pairs.

If we were to find the key by brute force, DES is easy. We can strengthen the DES algorithm by using nested ciphers. The tradeoff here is that these are slower than the original DES.

Define

• (2DES) $2E: \mathcal{K}^2 \times \mathcal{M} \rightarrow \mathcal{M}$ as $2E((k_1, k_2), m) = E(k_1, E(k_2, m))$.
• (3DES) $3E: \mathcal{K}^3 \times \mathcal{M} \rightarrow \mathcal{M}$ as $3E((k_1, k_2, k_3), m) = E(k_1, D(k_2, E(k_3, m)))$.⁴

Then the key space has increased (exponentially). As for 2DES, the key space is now $2^{112}$, so maybe nested ciphers increase the level of security.

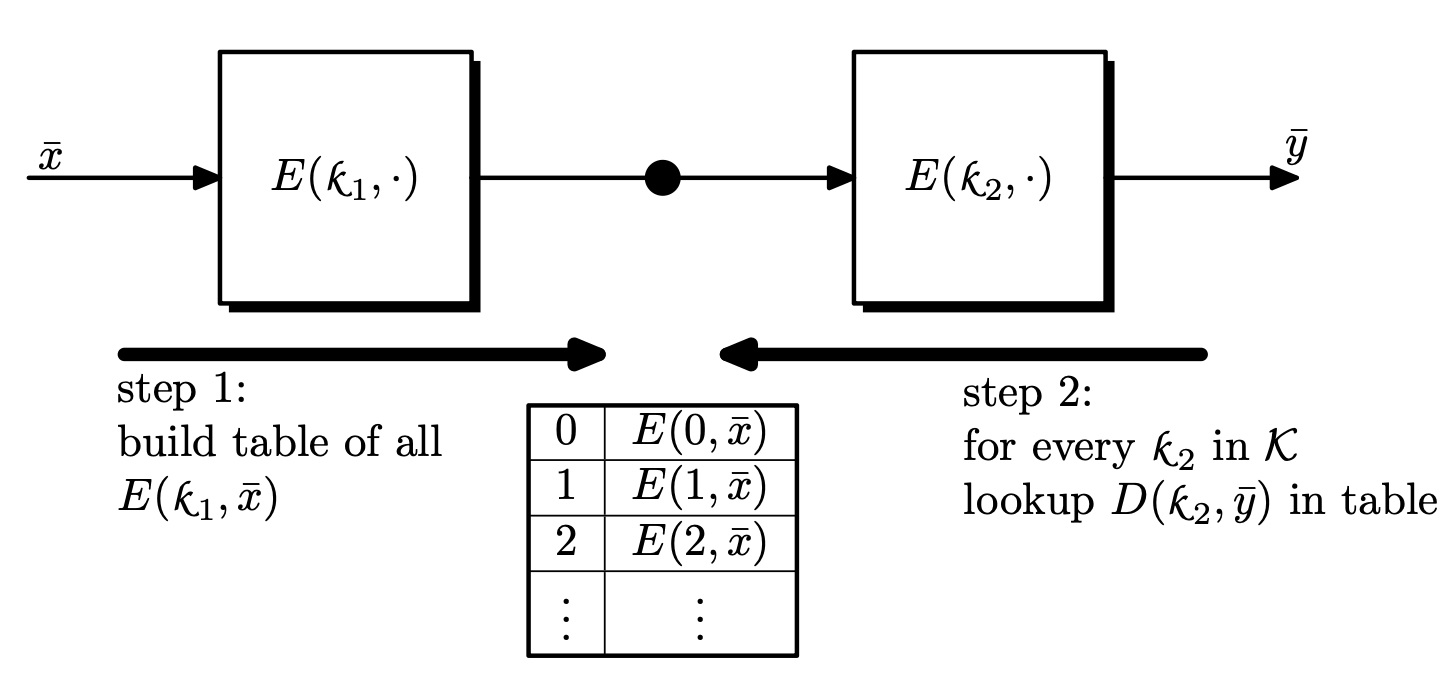
$2E$ is Insecure: Meet in the Middle

Unfortunately, 2DES is only secure as DES, with the attack strategy called meet in the middle. The idea is that if $c = E(k_1, E(k_2, m))$, then $D(k_1, c) = E(k_2, m)$.

Since we have the plaintext and the ciphertext, we first build a table of $(k, E(k_2, m))$ over $k_2 \in \mathcal{K}$ and sort by $E(k_2, m)$. Next, we check if $D(k_1, c)$ is in the table for all $k_1 \in \mathcal{K}$.

The complexity of this attack is shown as follows:

• Space complexity: We must store $\left\lvert \mathcal{K} \right\lvert$ entries with approximately $\log \left\lvert \mathcal{M} \right\lvert$ bits. Thus we need $\left\lvert \mathcal{K} \right\lvert \log \left\lvert \mathcal{M} \right\lvert$ bits in total.
• Time complexity: We run $E$ for $\left\lvert \mathcal{K} \right\lvert$ times and sorting takes $\left\lvert \mathcal{K} \right\lvert \log \left\lvert \mathcal{K} \right\lvert$. Searching the decrypted messages will also take $\left\lvert \mathcal{K} \right\lvert \log \left\lvert \mathcal{K} \right\lvert$.⁵

Considering DES, $\left\lvert \mathcal{K} \right\lvert = 2^{56}$ and $\left\lvert \mathcal{M} \right\lvert = 2^{64}$, the search space for the key is far less than $2^{112}$. Moreover, one would need a huge amount of memory to perform this attack, but time and space can be traded off.

3DES can be attacked in a similar manner, so the search space for the key is less than $2^{168}$, around $2^{112}$. It is currently infeasible to brute force this, so 3DES is used in practice.

The above argument can be generalized for any scheme $(E, D)$. Thus, the $2E$ construction is not secure.

$EX$ Construction and DESX

There is another method called the $EX$ construction for block cipher $(E, D)$ defined over $(\mathcal{K}, \mathcal{X})$. The $EX$ construction uses a new block cipher defined as follows. Intuitively, it can be thought of as applying OTP before and after encryption.

Let $k_1 \in \mathcal{K}$ and $k_2, k_3 \in \mathcal{X}$.

• Encryption: $EX\left((k_1, k_2, k_3), m\right) = E(k_1, m \oplus k_2) \oplus k_3$.
• Decryption: $DX((k_1, k_2, k_3), c) = D(k_1, c \oplus k_3) \oplus k_2$.

Then the new cipher $(EX, DX)$ has a key space $\mathcal{K} \times \mathcal{X}^2$, which is much larger than $\mathcal{K}$. Specifically for DESX, the key length would be $56 + 2 \times 64 = 184$ bits.

As a side note, using $E(k_1, m) \oplus k_2$ or $E(k_1, m \oplus k_2)$ does not improve security, since it can be attacked with meet in the middle method. Similarly, DESX also has $184$ bit key space, but actual search space is about $56 + 64 = 120$ bits.

Attacks on AES

The best known attack on AES is almost a brute force attack.

• AES-128 requires $2^{126.1}$ evaluations of AES.⁶
• AES-192 requires $2^{189.74}$ evaluations of AES.
• AES-256 requires $2^{254.42}$ evaluations of AES.

These are about $4$ times better than exhaustive search, so they have little impact on the security of AES.

There are also attacks with quantum computers, which uses an algorithm that can recover the key in time $\mathcal{O}(\sqrt{\left\lvert \mathcal{K} \right\lvert})$.⁷ We might need to use AES-256 when quantum computers are widely used.

1. The size of the lookup table is at least $\left\lvert X \right\lvert \log \left\lvert Y \right\lvert$ bits. The table should have at least $\left\lvert X \right\lvert$ rows, and each row must contain $\log \left\lvert Y \right\lvert$ bits of information. ↩︎

2. This method is even parallelizable! ↩︎

3. Note that $m$ has to be $\mathcal{O}(\log n)$ for $F$ to be efficient. ↩︎

4. We could also encrypt $3$ times. ↩︎

5. The running times of $E$ and $D$ were not considered here. ↩︎

6. A. Bogdanov, D. Khovratovich, and C. Rechberger. Biclique cryptanalysis of the full AES. In ASIACRYPT 2011, pages 344–371. 2011. ↩︎

7. L. K. Grover. A fast quantum mechanical algorithm for database search. In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, pages 212–219. ACM, 1996. ↩︎