Secure IAM on AWS with Multi-Account Strategy
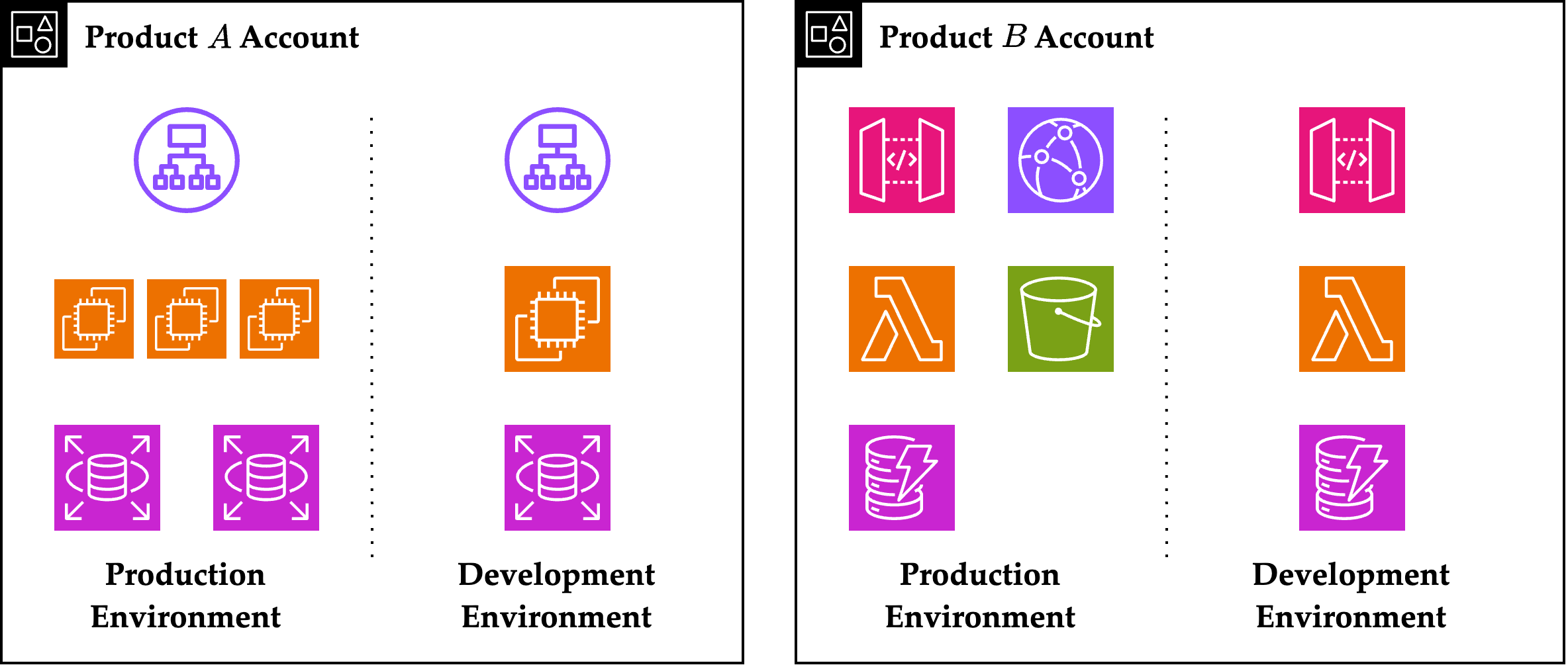
2024. 2. B.S. Graduation Paper, Received Best Paper Award! Secure IAM on AWS with Multi-Account Strategy (pdf) Presentation Poster (pdf) Abstract Many recent IT companies use cloud service...

2024. 2. B.S. Graduation Paper, Received Best Paper Award! Secure IAM on AWS with Multi-Account Strategy (pdf) Presentation Poster (pdf) Abstract Many recent IT companies use cloud service...
Here are the expected time complexities of the search operation in hash tables. Assumptions Let $m$ be the number of buckets in the hash table. Let $n$ be the number of entries currently in ...
Link to original text. I recommend reading the full text. It may seem a bit long but I assure you that it is worth the time. The talk is mainly about how to do first-class work, something signi...
Bootstrapping Recall that BGV has a limit on the number of operations, so it cannot evaluate a circuit with a large depth. This was because of the growing noise, so we need a way to remove the noi...
Homomorphisms Definition. Let $(X, \ast), (Y, \ast’)$ be sets equipped with binary operations $\ast$, $\ast’$. A map $\varphi : X \ra Y$ is said to be a homomorphism if \[\varphi(a \ast b) = \...
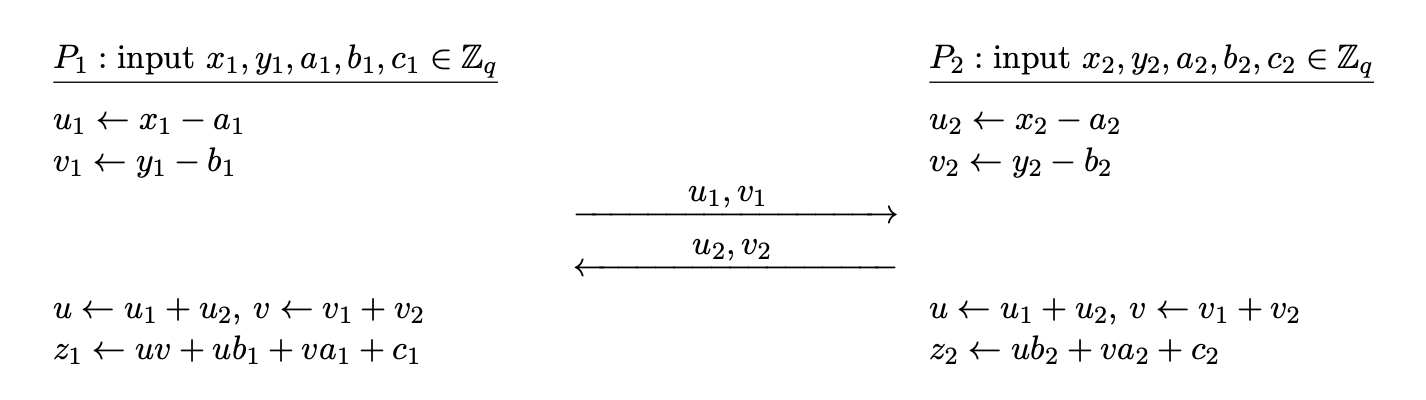
There are two types of MPC protocols, generic and specific. Generic protocols can compute arbitrary functions. Garbled circuits were generic protocols, since it can be used to compute any boolean c...
A simple solution for two party computation would be to use oblivious transfers as noted here. However, this method is inefficient. We will look at Yao’s protocol, presented in 1986, for secure two...
Secure Multiparty Computation (MPC) Suppose we have a function $f$ that takes $n$ inputs and produces $m$ outputs. [(y_1, \dots, y_m) = f(x_1, \dots, x_n).] $N$ parties $P_1, \dots, P_N$ are try...
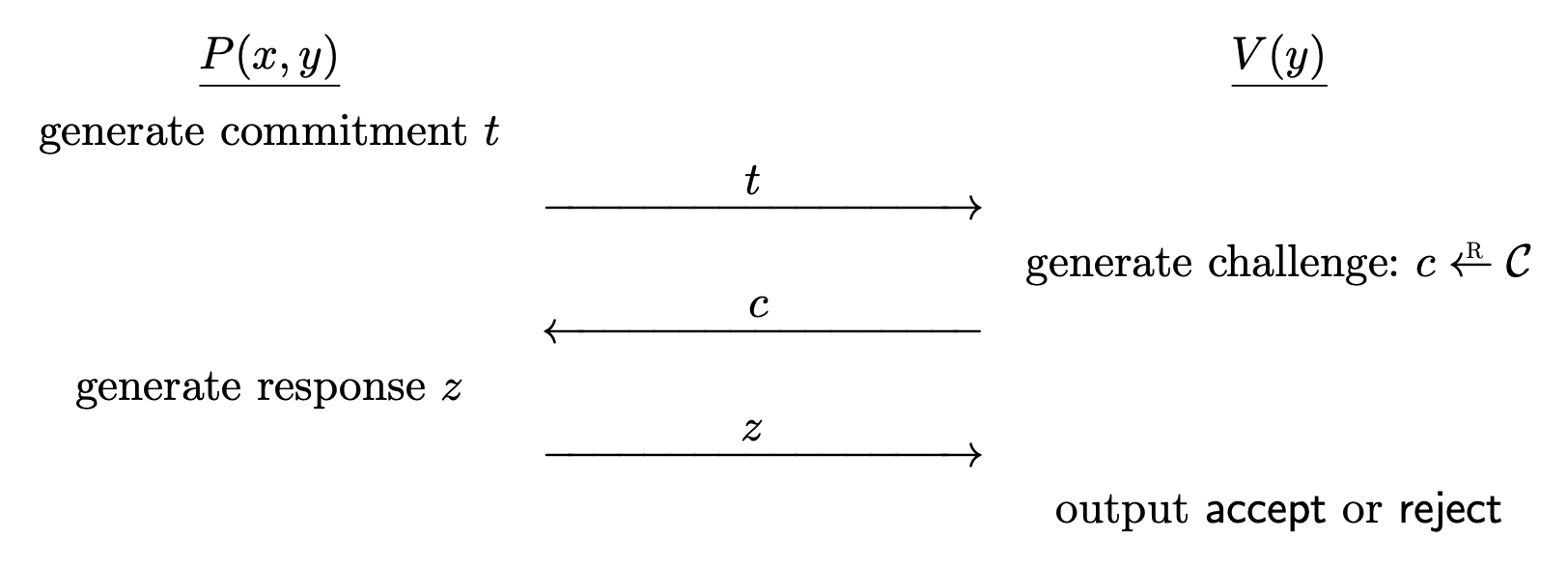
The previous 3-coloring example certainly works as a zero knowledge proof, but is quite slow, and requires a lot of interaction. There are efficient protocols for interactive proofs, we will study ...
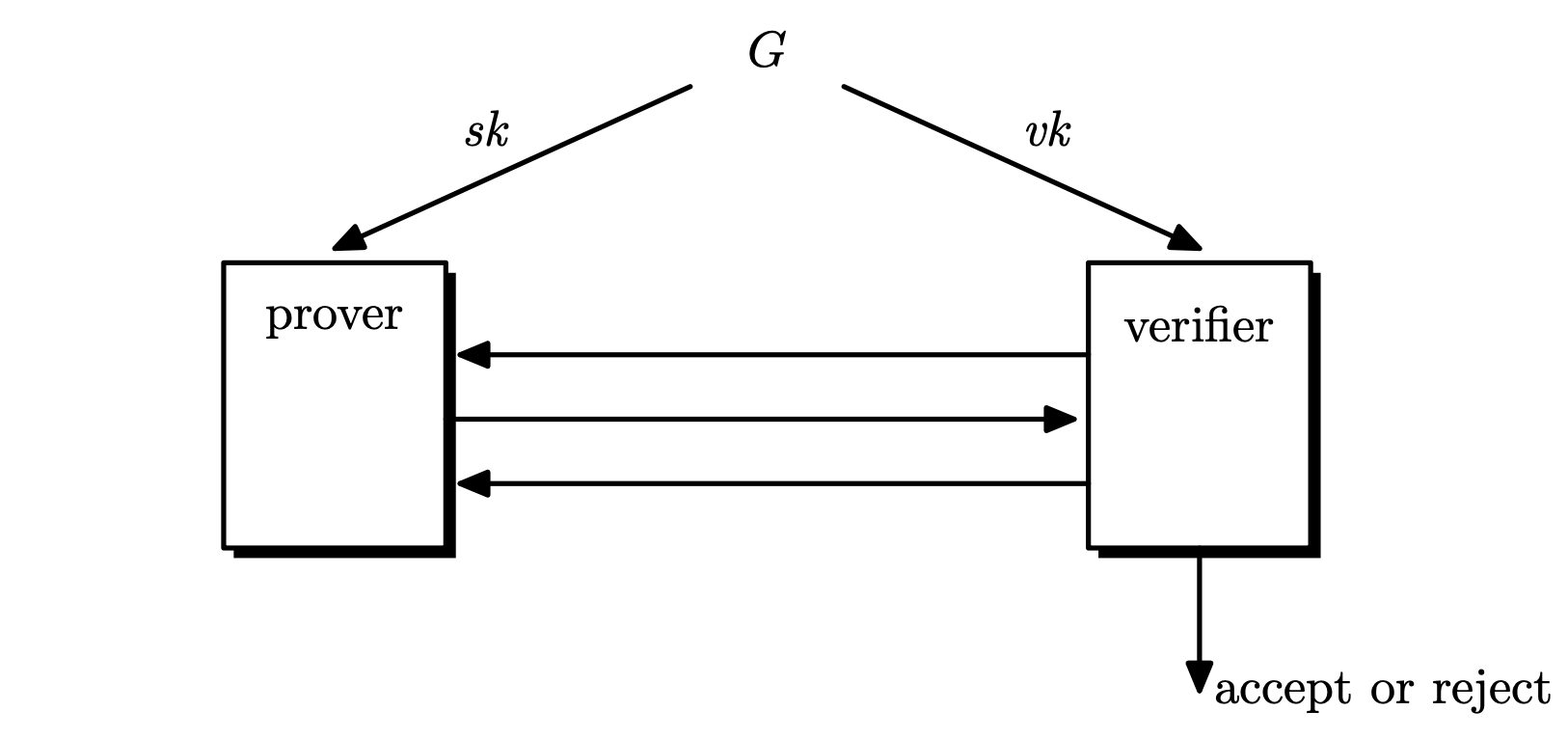
In 1980s, the notion of zero knowledge was proposed by Shafi Goldwasser, Silvio micali and Charles Rackoff. Interactive proof systems: a prover tries to convince the verifier that some statement ...