10. Digital Signatures

Digital Signatures

Definition. A signature scheme $\mc{S} = (G, S, V)$ is a triple of efficient algorithms, where $G$ is a key generation algorithm, $S$ is a signing algorithm, and $V$ is a verification algorithm.

• A probabilistic algorithm $G$ outputs a pair $(pk, sk)$, where $sk$ is called a secret signing key, and $pk$ is a public verification key.
• Given $sk$ and a message $m$, a probabilistic algorithm $S$ outputs a signature $\sigma \la S(sk, m)$.
• $V$ is a deterministic algorithm that outputs either $\texttt$ or $\texttt{reject}$ for $V(pk, m, \sigma)$.

The correctness property requires that all signatures generated by $S$ is always accepted by $V$. For all $(pk, sk) \la G$ and $m \in \mc{M}$,

\[\Pr[V(pk, m, S(sk, m)) = \texttt] = 1.\]

Properties of Digital Signatures

• Digital signatures can be verified by anyone, whereas MACs can be verified by the parties sharing the same key.
  • No need to share a key for digital signatures.
• Non-repudiation: cannot deny having created the signature.
  • Signatures can only be created by people having the secret key.
  • In cases where the secret key is leaked, then we don’t have non-repudiation.
  • In MACs, the secret key is shared by two parties, so we don’t have non-repudiation.
• Must trust the identity of the public key.
  • How do you trust that this public key is Alice’s?
  • We need public key infrastructure (PKI).

Applications

• Electronic document signing
• HTTPS/TLS certificates
• Software installation
• Authenticated email (DKIM)
• Bitcoins

Secure Digital Signatures

The definition is similar to the secure MAC. The adversary can perform a chosen message attack, but cannot create an existential forgery.

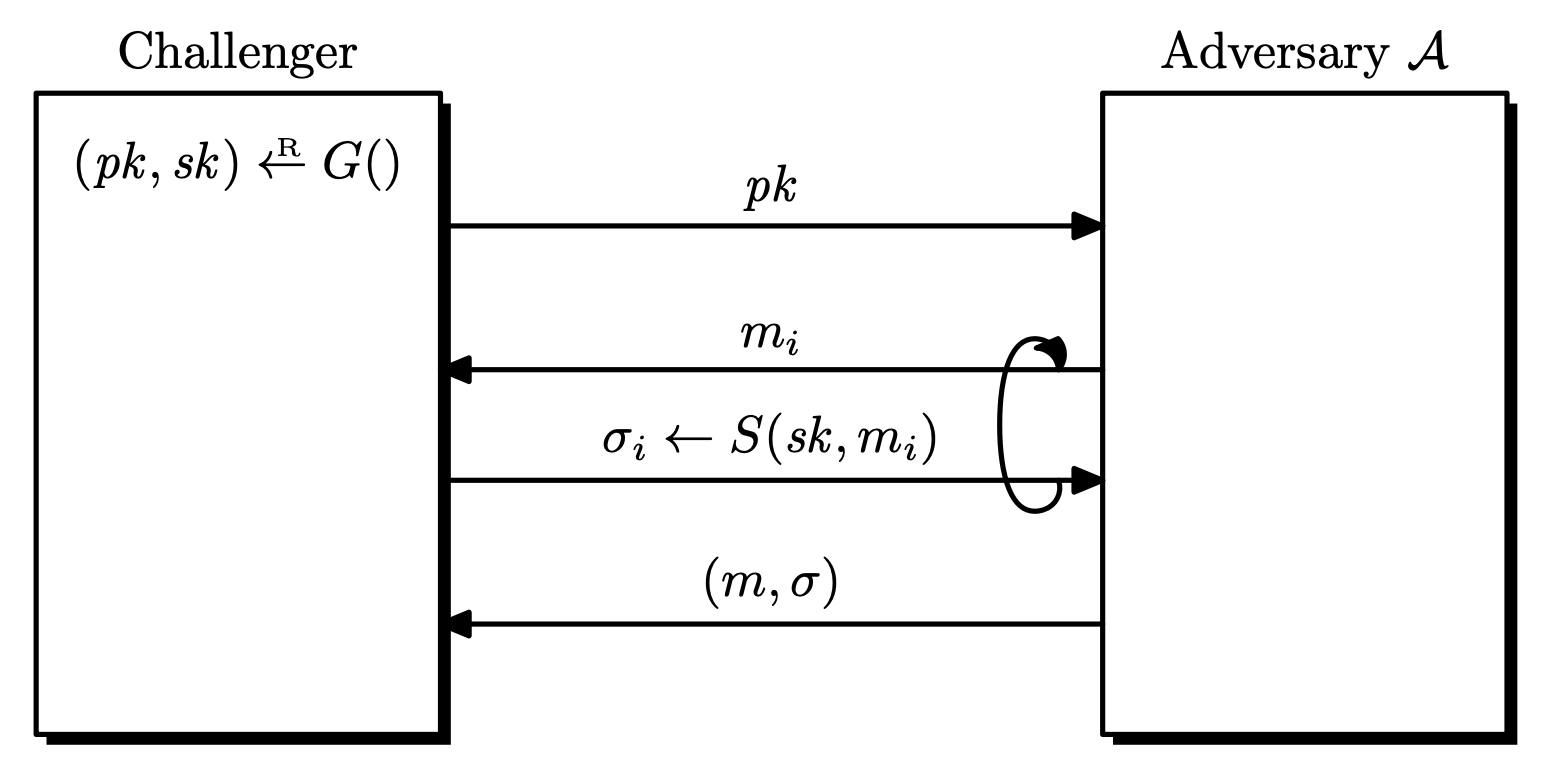
Definition. Let $\mc{S} = (G, S, V)$ be a signature scheme defined over $(\mc{M}, \Sigma)$. Given an adversary $\mc{A}$, the game goes as follows.

1. The challenger generates $(pk, sk) \la G()$ and sends $pk$ to $\mc{A}$.
2. $\mc{A}$ makes a series of signing queries to the challenger.
   • Each query is a message $m_i \in \mc{M}$, the challenger responds with $\sigma_i \la S(sk, m_i)$.
3. $\mc{A}$ computes and outputs a candidate forgery pair $(m, \sigma) \in \mc{M} \times \Sigma$.
   • $m \notin \left\lbrace m_1, \dots, m_q \right\rbrace$.
   • $(m, \sigma) \notin \left\lbrace (m_1, \sigma_1), \dots, (m_q, \sigma_q) \right\rbrace$. (strong)

$\mc{A}$ wins if $V(pk, m, \sigma) = \texttt{accept}$, let this event be $W$. The advantage of $\mc{A}$ with respect to $\mc{S}$ is defined as

\[\rm{Adv}_{\rm{SIG}}[\mc{A}, \mc{S}] = \Pr[W].\]

If the advantage is negligible for all efficient adversaries $\mc{A}$, the signature scheme $S$ is (strongly) secure. $\mc{S}$ is existentially unforgeable under a chosen message attack.

• We do not make verification queries, since the adversary can always check any signature.
• The normal definition of security is sufficient. Secure signature schemes can be converted into strongly secure signature schemes. See Exercise 14.10.¹

Message Confusion

Two different messages $m, m’$ can produce the same signature $\sigma$. In this case, the scheme is vulnerable to message confusion. See Exercise 13.3.¹

In common implementations, we consider $m$, $m’$ both to be valid. But there may be situations that this is undesirable. For those cases, a signature is would be a binding commitment to the message, and there will be no confusion.

Signer Confusion

Suppose that $(m, \sigma)$ is a valid pair with $pk$, i.e, $V(pk, m, \sigma) = \texttt{accept}$. But an attacker can generate $pk’$ different from $pk$ such that $V(pk’, m, \sigma) = \tt{accept}$. In this cases, we have signer confusion since both can claim to have signed $m$. See Exercise 13.4.¹

Strongly Binding Signatures

Strongly binding signatures prevent both message confusion and signer confusion.

Any signature scheme can be made strongly binding by appending a collision resistant hash of $(pk, m)$ to the signature. See Exercise 13.5.¹

Extending the Message Space

We can extend the message space of a secure digital signature scheme, as we did for MACs. Let $\mc{S} = (G, S, V)$ be a signature scheme defined over $(\mc{M}, \Sigma)$ and let $H : \mc{M}’ \ra \mc{M}$ be a hash function with $\left\lvert \mc{M}’ \right\lvert \geq \left\lvert \mc{M} \right\lvert$.

Define a new signature scheme $\mc{S}’ = (G, S’, V’)$ over $(\mc{M}’, \Sigma)$ as

\[S'(sk, m) = S(sk, H(m)), \qquad V'(pk, m, \sigma) = V(pk, H(m), \sigma).\]

This is often called the hash-and-sign paradigm, and the new signature scheme is also secure.

Theorem. Suppose that $\mc{S}$ is a secure signature scheme and $H$ is a collision resistant hash function. Then $\mc{S}’$ is a secure signature.

If $\mc{A}$ is an adversary attacking $\mc{S}’$, then there exist an adversary $\mc{B}_\mc{S}$ attacking $\mc{S}$ and an adversary $\mc{B}_H$ attacking $H$ such that

\[\rm{Adv}_{\rm{SIG}}[A, \mc{S}'] \leq \rm{Adv}_{\rm{SIG}}[\mc{B}_\mc{S}, \mc{S}] + \rm{Adv}_{\rm{CR}}[\mc{B}_H, H].\]

Proof. The proof is identical to the theorem for MACs.

Digital Signature Constructions

We can build secure signature schemes from hash functions, trapdoor permutations, or from discrete logarithms.

Textbook RSA Signatures

This is the signature scheme based on the textbook RSA. It is also insecure.

• Key generation: $pk = (N, e)$ and $sk = (N, d)$ are chosen to satisfy $d = e^{-1} \bmod \phi(N)$ for $N = pq$.
• Sign: $S(sk, m) = m^d \bmod N$.
• Verify: $V(pk, m, \sigma)$ returns $\texttt{accept}$ if and only if $\sigma^e = m \bmod N$.

Here are some possible attacks.

• No message attack
  • Just return $(\sigma^e, \sigma)$ for some $\sigma$. Then it passes verification.
• Attack using the homomorphic property.
  • Suppose we want to forge a message $m$.
  • Pick $m_1 \in \Z_N^{\ast}$ and set $m_2 = m\cdot m_1^{-1} \bmod N$.
  • Query signatures for both messages and multiply the responses.
    • $\sigma = \sigma_1 \cdot \sigma_2 = m_1^e \cdot m^e \cdot m_1^{-e} = m^e \bmod N$.
  • Then $(m, \sigma)$ is a valid pair.

Because of the second attack, the textbook RSA signature is universally forgeable. This property is used to create blind signatures, where the signer creates a signature without any knowledge about the message. See Exercise 13.15.¹

RSA Full Domain Hash Signature Scheme

Given a hash function $H : \mc{M} \ra \mc{Y}$, the RSA full domain hash signature scheme $\mc{S}_\rm{RSA-FDH}$ is defined as follows.

• Key generation: $pk = (N, e)$ and $sk = (N, d)$ are chosen to satisfy $d = e^{-1} \bmod \phi(N)$ for $N = pq$.
• Sign: $S(sk, m) = H(m)^d \bmod N$.
• Verify: $V(pk, m, \sigma)$ returns $\texttt{accept}$ if and only if $\sigma^d = H(m) \bmod N$.

This scheme is now secure.

Theorem. If the hash function $H$ is modeled as a random oracle, and the RSA assumptions holds, then $\mc{S}_\rm{RSA-FDH}$ is a secure signature scheme.

For any $q$-query adversary $\mc{A}$ against hashed RSA, there exists an adversary $\mc{B}$ solving the RSA problem such that

\[\rm{Adv}_{\rm{SIG}}[\mc{A}, \mc{S}_\rm{RSA-FDH}] \leq q \cdot \rm{Adv}_{\rm{RSA}}[\mc{B}].\]

Full Domain Hash Signature Scheme

The following is a description of a full domain hash scheme $\mc{S}_\rm{FDH}$, constructed from trapdoor permutation scheme $\mc{T} = (G, F, I)$.

• Key generation: $(pk, sk) \la G()$.
• Sign: $S(sk, m)$ returns $\sigma \la I(sk, H(m))$.
• Verify: $V(pk, m, \sigma)$ returns $\texttt{accept}$ if and only if $F(pk, \sigma) = H(m)$.

This scheme $\mc{S}_\rm{FDH} = (G, S, V)$ is secure if $\mc{T}$ is a one-way trapdoor permutation and $H$ is a random oracle.

Theorem. Let $\mc{T} = (G,F,I)$ be a one-way trapdoor permutation defined over $\mc{X}$. Let $H : \mc{M} \ra \mc{X}$ be a hash function, modeled as a random oracle. Then the derived FDH signature scheme $\mc{S}_\rm{FDH}$ is a secure signature scheme.

Proof. See Theorem 13.3.¹

Schnorr Digital Signature Scheme

This one uses discrete logarithms.

The Schnorr Identification Protocol

This scheme is originally from the Schnorr identification protocol.

Let $G = \left\langle g \right\rangle$ be a cyclic group of prime order $q$. We consider an interaction between two parties, prover $P$ and a verifier $V$. The prover has a secret $\alpha \in \Z_q$ and the verification key is $u = g^\alpha$. $P$ wants to convince $V$ that he knows $\alpha$, but does not want to reveal $\alpha$.

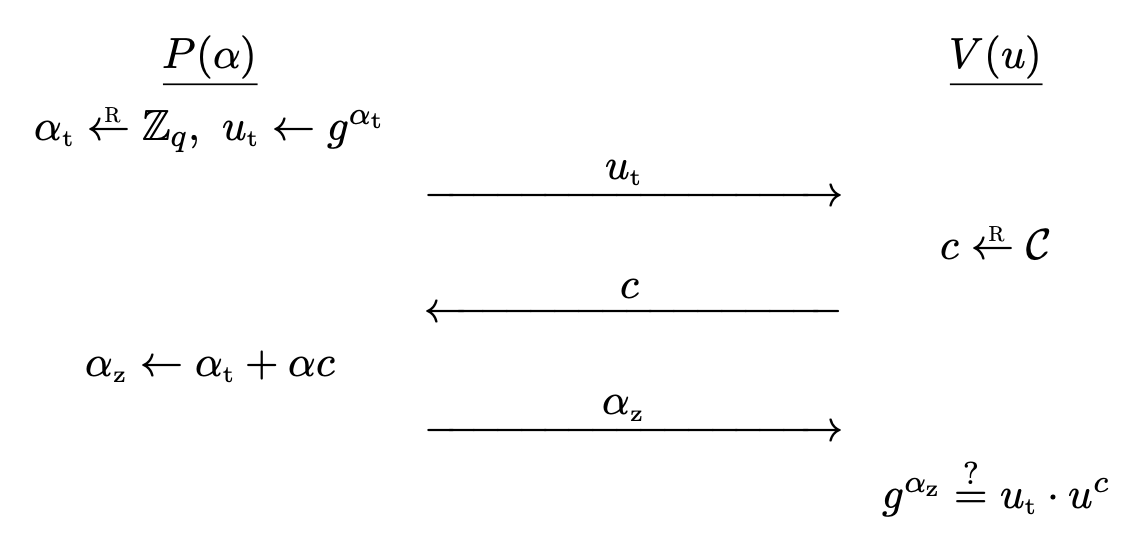
The protocol $\mc{I}_\rm{sch} = (G, P, V)$ works as follows.

1. A secret key $\alpha \la \Z_q$ and verification key $u \la g^\alpha$ is generated. The prover $P$ has $\alpha$ and the verifier $V$ has $u$.
2. $P$ computes a random $\alpha_t \la \Z_q$, and sends $u_t \la g^{\alpha_t}$ to $V$.
3. $V$ chooses a random $c \la \Z_q$ and sends it to $P$.
4. $P$ computes $\alpha_z \la \alpha_t + \alpha c \in \Z_q$ and sends it to $V$.
5. $V$ checks if $g^{\alpha_z} = u_t \cdot u^c$. Accept if and only if it is equal.

• $u_t$ is the commitment sent to the verifier.
• $c$ is the challenge sent to the prover.
  • If $P$ can predict the challenge, $P$ can choose $\alpha_t$ and $\alpha_z$ so that verifier accepts it.
• $\alpha_z$ is the response sent to the verifier.

We must check a few things.

• Correctness: If $P$ has the correct $\alpha$, then $g^{\alpha_z} = g^{\alpha_t} \cdot (g^\alpha)^c = u_t \cdot u^c$.
• Soundness: If $P$ does not have the correct $\alpha$, it is reject with probability $1 - \frac{1}{q}$.
  • We can repeat this many times then the probability of reject is $1 - \frac{1}{q^n} \ra 1$.
  • Thus $q$ (the size of the challenge space) must be large.
• Zero-knowledge: $V$ learns no information about $x$ from the conversation.
  • This will be revisited later. See here.

Theorem. The Schnorr identification protocol is secure if the DL problem is hard, and the challenge space $\mc{C}$ is large.

Schnorr Digital Signature Scheme

We transform the above protocol to a signature scheme.² We need a hash function $H : \mc{M} \times G \ra \mc{C}$, modeled as a random oracle. The protocol originally involves interaction between two parties, but a signature is computed by a single party. Intuitively, $H$ will play the role of the verifier.

The Schnorr signature scheme $\mc{S}_\rm{sch} = (G, S, V)$ is defined as follows.

• Key generation: a secret key $sk = \alpha \la \Z_q$ and public key $pk = u \la g^\alpha$ is generated.
• Sign: $S(sk, m)$ outputs $\sigma = (u_t, \alpha_z)$ where
  • Choose random $\alpha_t \la \Z_q$ and set $u_t \la g^{\alpha_t}$.
  • Compute $c \la H(m, u_t)$ and set $\alpha_z \la \alpha_t + \alpha c$.
• Verify: $V(pk, m, \sigma)$ outputs $\texttt{accept}$ if and only if $g^{\alpha_z} = u_t \cdot u^c$.
  • $c \la H(m, u_t)$ can be computed and $u$ is known.

Since $H$ is being modeled as a random oracle, the signer cannot predict the value of the challenge $c$. Also, $c$ must take both $m$ and $u_t$ as input, since without $m$, the signature is not related to $m$ (the signature has no $m$ term inside it). On the other hand, without $u_t$, then the scheme is insecure since the Schnorr identification protocol is HVZK. See Exercise 19.12.¹

Theorem. If $H$ is modeled as a random oracle and Schnorr’s identification protocol is secure, then Schnorr’s signature scheme is also secure.

Proof. See Theorem 19.7.¹

Note that $\alpha \la \Z_q$ must be chosen randomly every time.

Digital Signature Algorithm

Schnorr’s scheme was protected by a patent, so NIST opted for a ad-hoc signature scheme based on a prime order subgroup of $\Z_p^{\ast}$. This algorithm eventually became the Digital Signature Algorithm (DSA). The standard was updated to support elliptic curve groups over a finite field, resulting in ECDSA.

Public Key Infrastructure

How would you trust public keys? We introduce digital certificates for this.

Read in public key infrastructure (Internet Security).

1. A Graduate Course in Applied Cryptography ↩︎ ↩︎² ↩︎³ ↩︎⁴ ↩︎⁵ ↩︎⁶ ↩︎⁷ ↩︎⁸

2. By using the Fiat-Shamir transform. ↩︎