05. Lebesgue Integration
Lebesgue Integration
르벡 적분을 단계적으로 정의하려고 합니다. $X = (X, \mathscr{F}, \mu)$ 라고 계속 가정합니다. $\mathscr{F}$는 $\sigma$-algebra on $X$, $\mu$는 $\mathscr{F}$의 measure 입니다.
$E \in \mathscr{F}$ 일 때, 적분을 정의하기 위해
\[\mathscr{F} _ E = \lbrace A \cap E : A \in \mathscr{F}\rbrace, \quad \mu_E = \mu|_ {\mathscr{F} _ E}\]로 설정하고 $\int = \int_E$ 로 두어 ($X, \mathscr{F} _ E, \mu_E$) 위에서 적분을 정의할 수 있습니다. 그러나 굳이 이렇게 하지 않아도 됩니다. $\int = \int_X$ 로 두고
\[\int_E f \,d{\mu} = \int f \chi _E \,d{\mu}\]로 정의하면 충분하기 때문입니다.
르벡 적분을 다루기 위해 simple function부터 적분해보겠습니다.
Step 1. For Characteristic Functions
우선 가장 간단한 characteristic function부터 단계를 밟아나가야 합니다.
(Step 1) $A \in \mathscr{F}$ 에 대하여
\[\int \chi_A \,d{\mu} = \mu(A)\]로 정의한다.
함수 $\chi_A$는 $x \in A$ 일 때만 함숫값 $1$을 갖고 이외의 경우에는 $0$이기 때문에 이 함수를 $X$ 위에서 적분하면 ‘$A$의 길이’에 대응되는 $\mu(A)$가 결과인 것이 자연스럽습니다.
Step 2. For Positive Measurable Simple Functions
다음으로 양의 값을 갖는 measurable simple function에 대해 정의합니다. $f = f^+ - f^-$ 에서 $f^+, f^-$ 모두 양의 값을 갖기 때문에 양의 값에 대해 먼저 정의합니다.
(Step 2) $f: X \rightarrow[0, \infty)$ 가 measurable simple function이라 하자. 그러면 $A_k \subseteq\mathscr{F}$ 이면서 쌍마다 서로소인 집합열 $\left( A_k \right) _ {k=1}^n$과 $a_k \in [0, \infty)$ 인 수열 $\left( a_k \right) _ {k=1}^n$을 잡아
\[f(x) = \sum_ {k=1}^n a_k \chi_ {A_k}\]와 같이 표현할 수 있다. 이제
\[\int f\,d{\mu} = \sum_ {k=1}^n a_k \mu(A_k) \in [0, \infty]\]로 정의한다.
Measurable simple function은 measurable characteristic function의 linear combination으로 표현할 수 있기 때문에, 이와 같은 정의를 생각할 수 있습니다. 하지만 이런 정의를 보면 well-definedness를 제일 먼저 생각해야 합니다. 위와 같은 linear combination 표현이 유일하지 않기 때문입니다.
Well-definedness를 증명하기 위해 임의의 linear combination을 잡아도 적분값이 항상 같음을 보이면 됩니다.
명제. 위 정의는 모든 measurable simple function에 대해 well-defined이다.
증명. $f$가 다음과 같이 두 가지 방법으로 표현된다고 하자.
\[f(x) = \sum_ {k=1}^n a_k \chi_ {A_k} = \sum_ {i=1}^m b_i \chi_ {B_i}.\]여기서 $k = 1, \dots, n$, $i = 1, \dots, m$ 에 대하여 $0\leq a_k, b_i < \infty$ 이고 $A_k, B_i \in \mathscr{F}$ 이다. 여기서 $A_k, B_i$는 각각 쌍마다 서로소로, $X$의 분할이 된다. $C_ {k, i} = A_k \cap B_i$ 로 두면
\[\sum_ {k=1}^n a_k \mu(A_k) = \sum_ {k=1}^n a_k \mu\left( A_k \cap \bigcup_ {i=1}^m B_i \right) = \sum_ {k=1}^n \sum_ {i=1}^m a_k \mu(C_ {k, i}),\] \[\sum_ {i=1}^m b_i \mu(B_i) = \sum_ {i=1}^{m} b_i \mu\left( B_i \cap \bigcup_ {k=1}^n A_k \right)= \sum_ {i=1}^m \sum_ {k=1}^n b_i \mu(C_ {k, i})\]이다. 이 때 $C_ {k, i} \neq \varnothing$ 이면 $x \in C_ {k, i}$ 에 대해 $f(x) = a_k = b_i$ 가 된다. 한편 $C_ {k, i} = \varnothing$ 이면 $\mu(C_ {k, i}) = 0$ 이다. 이로부터 모든 $k, i$에 대하여 $b_i \mu(C_ {k, i}) = a_k \mu(C_ {k, i})$ 임을 알 수 있다.1 따라서
\[\int f \,d{\mu }= \sum_ {k=1}^n a_k \mu(A_k) = \sum_ {i=1}^m b_i \mu(B_i)\]가 되어 적분값은 유일하고 위 정의가 well-defined임을 알 수 있다.
이제 measurable simple function은 얼마든지 적분할 수 있습니다. 이제 다음은 measurable function으로 확장할 단계입니다. 확장을 편하게 하기 위해 약간의 준비 작업을 거치겠습니다.
적분은 선형이고, monotonicity를 항상 유지하기를 기대합니다. 아직은 함수가 $0$보다 클 것을 가정했기 때문에 이를 계속 활용합니다.
참고. $a, b \in [0, \infty)$ 와 measurable simple function $f, g \geq 0$ 에 대하여
\[\int \left( af + bg \right) \,d{\mu} = a \int f \,d{\mu} + b \int g \,d{\mu}\]이다.
증명. 위 Step 2와 동일하게
\[f = \sum_ {j=1}^m y_j \chi_ {A_j}, \quad g = \sum_ {k=1}^n z_k \chi_ {B_k}\]로 둘 수 있다. 여기서 $A_j, B_k$는 $X$의 분할이고 $y_j, z_k \geq 0$ 이다. 마찬가지로 $C_ {j, k} = A_j \cap B_k$ 로 정의하면
\[\begin{aligned} a \int f \,d{\mu} + b \int g \,d{\mu} & = \sum_ {j} ay_j \mu(A_j) + \sum_k b z_k \mu(B_k) \\ & = \sum_ {j} ay_j \sum_k \mu(A_j \cap B_k) + \sum_k b z_k \sum_j \mu(B_k \cap A_j) \\ & = \sum_ {j} \sum_k ay_j \mu(C_ {j, k}) + \sum_k \sum_j b z_k \mu(C_ {j, k}) \\ & = \sum_ {j, k} (ay_j + bz_k) \mu(C_ {j, k}) = \int \left( af + bg \right) \,d{\mu} \end{aligned}\]이다.
참고. $f \geq g \geq 0$ 이 measurable simple function일 때,
\[\int f \,d{\mu} \geq \int g \,d{\mu}\]이다.
증명. $f - g \geq 0$ 이 simple이고 measurable임을 활용한다.
\[\int f \,d{\mu} = \int \left[g + (f - g)\right] \,d{\mu} = \int g\,d{\mu} + \int (f - g) \,d{\mu} \geq \int g \,d{\mu} \geq 0.\]위와 같이 $g + (f-g)$ 로 변형해야 하는 이유는 $g$의 적분값이 무한대인 경우 이를 이항할 수 없기 때문입니다. 하지만 $f-g$ 의 적분값이 $0$ 이상인 것은 확실하게 알 수 있습니다.
Step 3. For Positive Measurable Functions
이제 양의 값을 가지는 임의의 measurable function을 고려해 보겠습니다.
(Step 3) $f: X \rightarrow[0, \infty]$ 가 measurable일 때,
\[\int f \,d{\mu} = \sup\left\lbrace \int h \,d{\mu}: 0\leq h \leq f, h \text{ measurable and simple}\right\rbrace.\]로 정의한다.
$f$보다 작은 measurable simple function의 적분값 중 상한을 택하겠다는 의미입니다. $f$보다 작은 measurable simple function으로 $f$를 근사한다고도 이해할 수 있습니다. 또한 $f$가 simple function이면 Step 2의 정의와 일치하는 것을 알 수 있습니다.
$f \geq 0$ 가 measurable이면 증가하는 measurable simple 함수열 $s_n$이 존재함을 지난 번에 보였습니다. 이 $s_n$에 대하여 적분값을 계산해보면
\[\int_E s_n \,d{\mu} = \sum_ {i=1}^{n2^n} \frac{i - 1}{2^n}\mu\left( \left\lbrace x \in E : \frac{i-1}{2^n} \leq f(x) \leq \frac{i}{2^n}\right\rbrace \right) + n\mu(\lbrace x \in E : f(x)\geq n\rbrace)\]임을 알 수 있습니다. 이제 $n \rightarrow\infty$ 일 때 우변이 곧 $\displaystyle\int f \,d{\mu}$ 이기를 기대합니다.
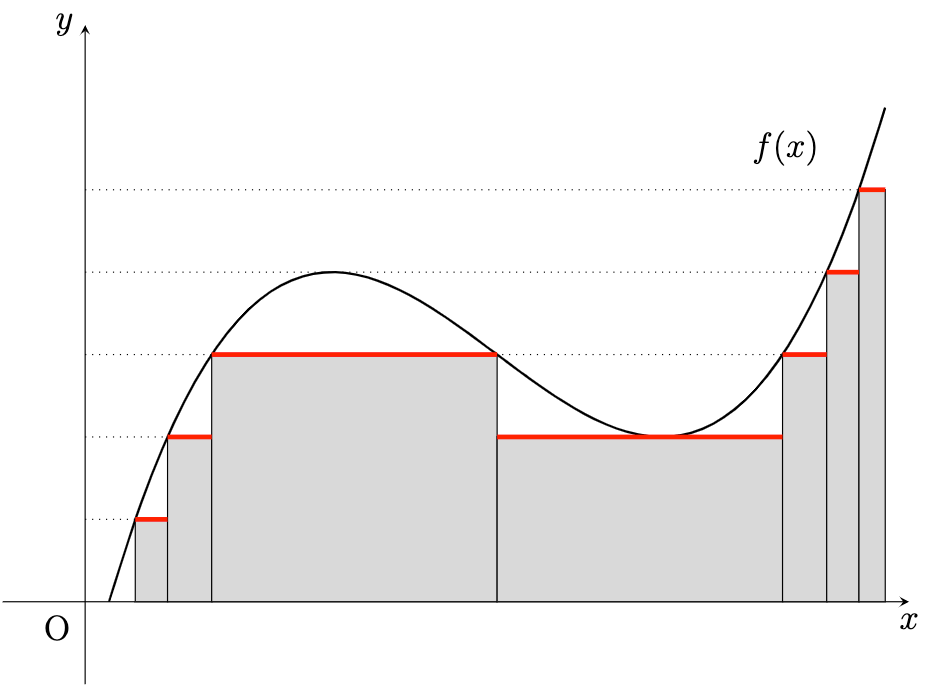
위 내용에 대한 증명은 추후 다루도록 하고 식의 의미를 이해해 보겠습니다. 르벡 적분은 치역을 잘게 잘라 자른 치역 부분의 preimage에 대해 measure를 사용하여 길이를 잽니다. 그리고 함숫값과 preimage의 measure를 곱한 뒤 더해 넓이를 계산한다고 이해할 수 있습니다. 리만 적분은 정의역을 잘게 잘라 상합/하합을 고려하여 정의한 것과는 다른 접근 방법입니다.
Step 4. For Measurable Functions
이제 마지막 단계입니다. 임의의 measurable function에 대해 정의합니다.
(Step 4) $f$가 measurable이면 $f^+, f^- \geq 0$ 도 measurable이다. 그러므로 $E \in \mathscr{F}$ 에 대하여
\[\int_E f \,d{\mu} = \int_E f^+ \,d{\mu} - \int_E f^- \,d{\mu}\]와 같이 정의한다. 단, 우변에서 $\infty - \infty$ 가 등장하는 경우는 제외한다.
우변에서 $\infty - \infty$ 인 경우는 제외되었기 때문에 $f^+$, $f^-$의 적분값 둘 중 하나는 유한해야 합니다.
Lebesuge Integrable
위 내용을 종합하여 다음 정의를 얻습니다.
정의. (르벡 적분 가능) $f$가 measurable이고,
\[\int_E \lvert f \rvert \,d{\mu} = \int_E f^+ \,d{\mu} + \int_E f^- \,d{\mu} < \infty\]이면 $f$가 $E$에서 $\mu$에 대해 르벡 적분 가능하다고 한다.
표기법. $f$가 $E$에서 $\mu$에 대해 르벡 적분 가능하면
\[f \in \mathcal{L}^1(E, \mu)\]로 표기한다. 특별히 $\mu = m$ 이면 $f \in \mathcal{L}^1(E)$ 로 적는다.
즉 다음이 성립합니다.
\[f \in \mathcal{L}^{1}(E, \mu) \iff f^+, f^- \in \mathcal{L}^{1}(E, \mu)\iff \lvert f \rvert \in \mathcal{L}^{1}(E, \mu).\]계수가 같거나, measure가 0이 되어 같거나. ↩︎