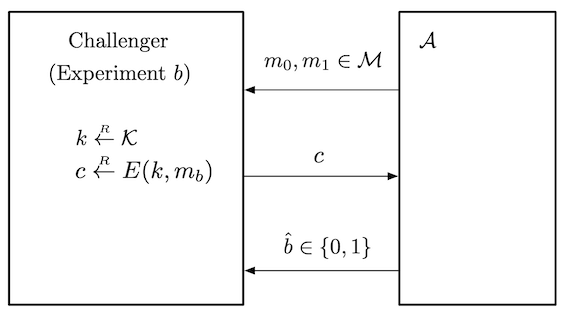
1. One-Time Pad, Stream Ciphers and PRGs
Assumptions and Notations An encryption scheme is defined by $3$ algorithms. A (probabilistic) key generation algorithm $G$. $E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}$ and $...

Assumptions and Notations An encryption scheme is defined by $3$ algorithms. A (probabilistic) key generation algorithm $G$. $E: \mathcal{K} \times \mathcal{M} \rightarrow \mathcal{C}$ and $...
Classical Cryptography The “art” of writing or solving codes - Oxford Art focusing on ensuring private communication between two parties. Two parties share secret information in advance....
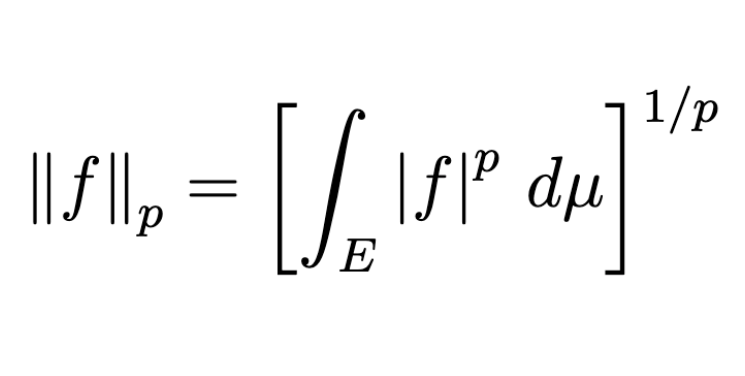
Integration on Complex Valued Function Let $(X, \mathscr{F}, \mu)$ be a measure space, and $E \in \mathscr{F}$. 정의. A complex valued function $f = u + iv$, (where $u, v$ are real functio...
This is a list of proofs with Coq, for each rule of inference stated in List of Rules of Inference (Wikipedia) Some rules that need the law of excluded middle are at the end of the section. Rules...

New blog logo 오래 전, Github Pages가 불편하다는 이유로 티스토리로 옮겼었다. 근데 어쩌다 보니 결국 다시 돌아오게 되었다. History 2019년 12월에 calofmijuck.github.io 사이트를 세팅했었다. 하지만 여러 불편한 점들을 발견했고, Jekyll 문서를 열심히 읽어보고 커스터마이즈를 시도한 끝에 실패하...
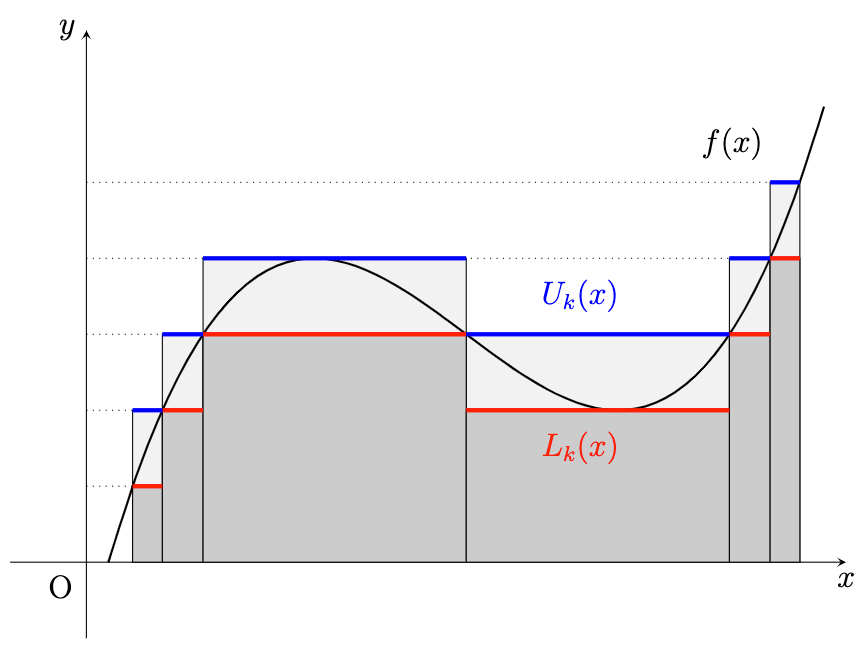
Comparison with the Riemann Integral 먼저 혼동을 막기 위해 Lebesgue measure $m$에 대하여 르벡 적분을 [\int_ {[a, b]} f \,d{m} = \int_ {[a, b]} f \,d{x} = \int_a^b f \,d{x}] 와 같이 표기하고, 리만 적분은 [\mathcal{R}\int_a^b...
Almost Everywhere 지난 글에서 measure가 0인 집합 위에서 적분하면 결과가 0이 됨을 확인했습니다. 적분 입장에서 보면 measure가 0인 곳에서의 적분은 의미가 없다고 생각할 수 있겠죠? 그러면 앞으로 그런걸 무시해도 된다고 하면 어떨까요? 정의. (Almost Everywhere) $P = P(x)$ 가 어떤 성질이라 하자...
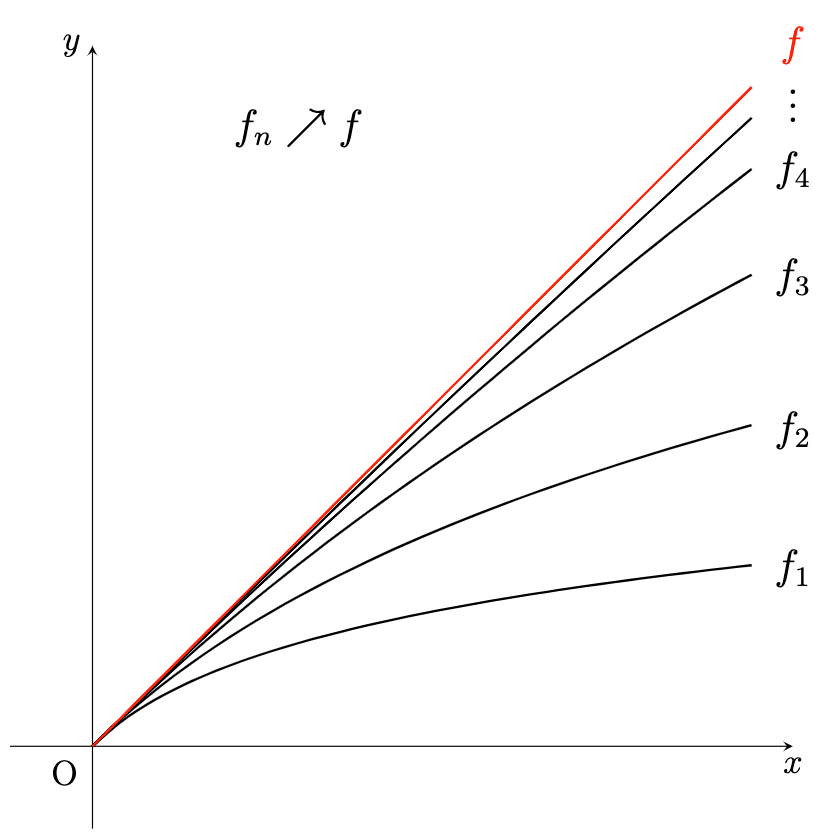
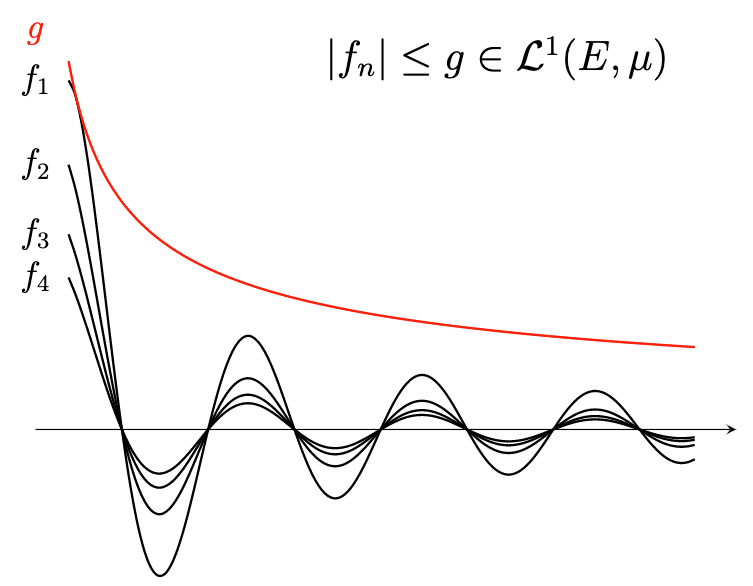
르벡 적분 이론에서 굉장히 자주 사용되는 수렴 정리에 대해 다루겠습니다. 이 정리들을 사용하면 굉장히 유용한 결과를 쉽게 얻을 수 있습니다. Monotone Convergence Theorem 먼저 단조 수렴 정리(monotone convergence theorem, MCT)입니다. 이 정리에서는 $f_n \geq 0$ 인 것이 매우 중요합니다. ...
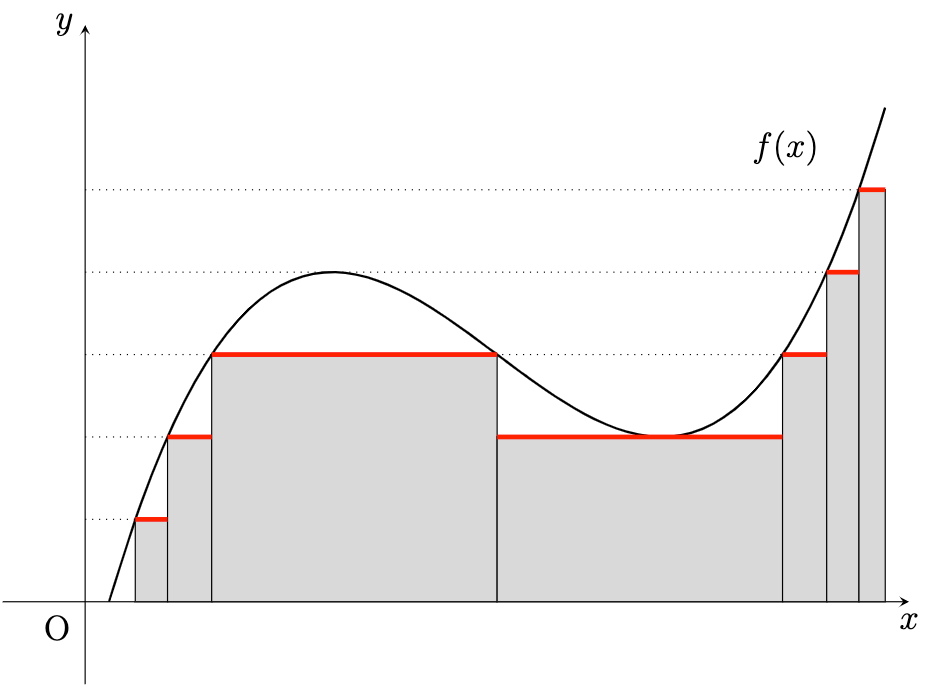
Lebesgue Integration 르벡 적분을 단계적으로 정의하려고 합니다. $X = (X, \mathscr{F}, \mu)$ 라고 계속 가정합니다. $\mathscr{F}$는 $\sigma$-algebra on $X$, $\mu$는 $\mathscr{F}$의 measure 입니다. $E \in \mathscr{F}$ 일 때, 적분을 정의하기 ...
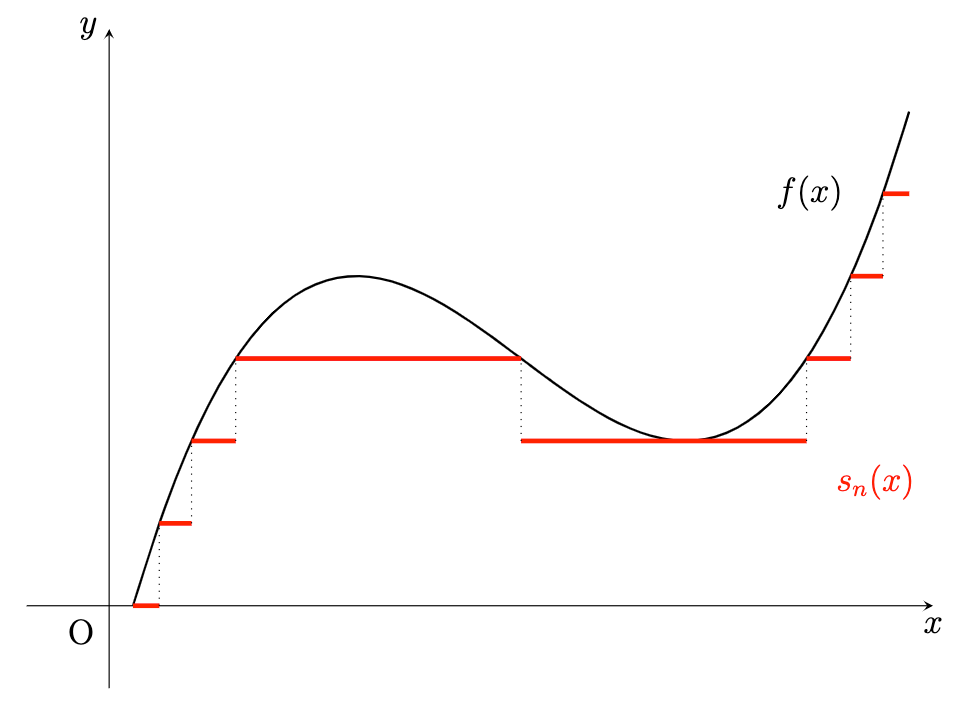
Lebesgue integral을 공부하기 전 마지막 준비입니다. Lebesgue integral은 다음과 같이 표기합니다. [\int_X f \,d{\mu}] 표기를 보면 크게 3가지 요소가 있음을 확인할 수 있습니다. 바로 집합 $X$, measure $\mu$, 그리고 함수 $f$입니다. 집합과 measure는 다루었으니 마지막으로 함수에 관...